Department of Mechanics, Milan’s Polytechnic
We asked the Department of Mechanics at Milan’s Polytechnic, in the person of Prof. Francesco Braghin, to measure the stresses an Olympic barbell undergoes during the main exercises: bench press, deadlift, squat, snatch and sprint. The objective is extremely practical; to define simple and usable multiplication coefficients, even approximate, useful to the athlete in considering the stress of the discs loaded on the barbell according to the performed exercises.

The activity concerned the ‘sensorization’ of three different models of Olympic barbells; 9015/4, 9015/5, 9015/9, by technicians from the Department of Mechanics of Milan’s Polytechnic, who are qualified to bond strain gauge sensors.
Considering that the bending stresses on the rocker arm stem
- from the weight forces at both ends, corresponding to the weight of the sleeves and weights;
- from the forces exerted by the athlete’s hands to lift the barbell
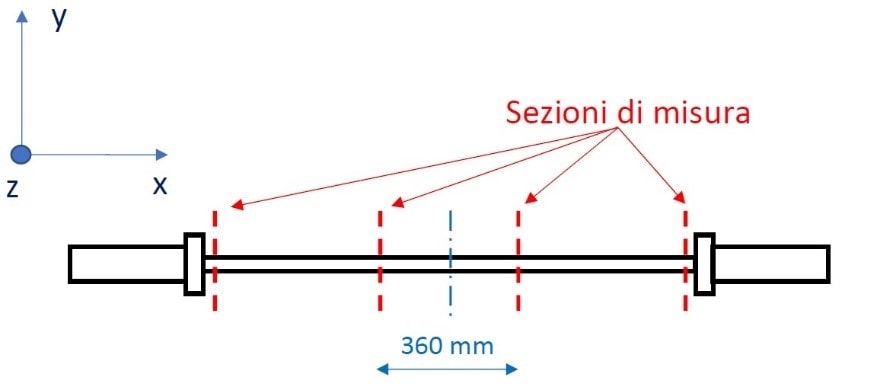
it was deemed necessary to instrument the bar in 4 different sections
- two sections at the end of the barbell, i.e. the point as close as possible to the sleeve, compatible with the dimensions of the strain gauge and its electrical connections; these sections are therefore between the sleeve and the athlete’s grip
- two sections over the barbell centre and symmetrical with respect to it, i.e. within the athlete’s grip points; for all the instrumented barbells, the distance between these sections turned out to be 360 mm.
.
Being concerned only with the bending of the barbell, it was possible to construct a system for measuring deformations using two complete strain gauge bridges for each section:
- No. 1 complete bridge along the horizontal plane (XZ);
- No. 1 complete bridge along the vertical plane (XY).
The use of complete strain gauge bridges, realised with two strain gauges orthogonal to each other placed on the two generators of the barbell belonging to a diametrical plane, has allowed to make the measurement insensitive to axial action and temperature variations. The figure shows the diagram for the positioning of the strain gauges on the measuring section. Each blue patch in the figure contains the pair of orthogonal strain gauges described above.

In total, therefore, eight 10-metre-long cables (in order to give the athlete sufficient comfort) corresponding to the eight measuring channels (bending along two directions for four measuring sections) branch off from each barbell.
We performed a simple test for strain gauge bridge resetting: the barbell was placed in a vertical position (i.e. the position corresponding to a zero bending moment on all four measuring sections), the output of the bridges (offset) was measured and this value was then subtracted from the measurements to be taken from there on.
Each test was carried out at a sampling frequency of 5 kHz, in order to measure not only the stresses due to the athlete’s gestures, but also those of an impulsive nature due, for example, to the barbell falling to the ground.
Conclusions:
From the tests performed on the three barbells, it should be botice what was to be expected: the most dynamic exercises, with higher accelerations, resulted in the highest stress values. Obviously maximum stress and extended to all the sensors, in the event of the barbell falling, although in this case the maximum strain values were very different as a result of the way the barbell struck the ground.

As for the definition of the multiplication coefficients, the test showed:
- snatch and momentum x 3.0
- squat x 1.8
- bench press x 1.7
- deadlift x 1.5
Therefore, taking the snatch and momentum exercise as an example, 100 kg of discs loaded on the Olympic barbell will carry out a force weight corresponding to 300 kg.
Beware of falling from above! The multiplication coefficient turned out to be x 3.25, but as we have said, it undergoes several variables.
Also pay attention to the performance of the exercises. During the test, we stuck to ‘standard’ executions, or as standard as possible. Squats and deadlifts, but also bench presses, can be performed with high acceleration, explosively, and this inevitably raises the multiplication coefficients.
































